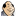This demo computes the Mandelbrot set. Its numerical calculation can be easily parallelized.
Up to four threads, each of them is coded in another programming language,
compute one horizontal part of this fractal.
Use the mouse to enhance any part of this graphical representation:
-
If the mouse pointer is over the fractal image, labelled Mandelbrot set,
a crosshair cursor will appear.
-
Press the left mouse button to determine the upper left corner of the part which is to be enlarged.
Move the mouse pointer to the chosen lower right corner of the part which is to be enlarged. Then press the left mouse button again.
- Now the range of the Mandelbrot set will be computed according to the selected rectangle.
-
Alternatively, you can alter the range manually via the appropriate input fields.
-
Click the Compute button to generate a Mandelbrot set that matches the changed range.
-
The Reset button restores the initial range and the corresponding fractal image.
Java Source:
/*
* fractal demo
* written by Peter Sauer
* ScienceSoft 2003,2004
*/
public int[] doCalc(
int yOffset,
int lines,
int width,
int maxIter,
double xStart,
double xZoom,
double yStart,
double yZoom) {
int buffer[] = new int[lines * width];
int index = 0;
for (int y = yOffset; y < yOffset + lines; ++y) {
double tmp = yStart + yZoom * (double) y;
for (int x = 0; x < width; ++x) {
double r = 0.0, i = 0.0, m = 0.0;
int iter = 0;
while ((iter < maxIter) && (m < 4.0)) {
m = r * r - i * i;
i = 2.0 * r * i + tmp;
r = m + xStart + xZoom * (double) x;
++iter;
}
buffer[index++] = iter * iter;
}
}
return buffer;
}
C Source:
/*
* fractal demo
* written by Peter Sauer
* ScienceSoft 2003,2004
*/
JNIEXPORT jintArray JNICALL Java_fractal_NativeCWorkerThread_doCalc(
JNIEnv *env, jobject obj,jint yOffset, jint lines, jint width, jint maxIter,
jdouble xStart, jdouble xZoom, jdouble yStart, jdouble yZoom) {
jint *buffer = (jint *)malloc(lines * width * sizeof(jint));
jint index = 0;
jint y,x;
jintArray array;
jint end = yOffset + lines;
if(!buffer) {
return NULL;
}
for(y = yOffset; y < end ; ++y) {
jdouble tmp = yStart + yZoom * (double) y;
for (x = 0; x < width; ++x) {
jdouble r = 0.0, i = 0.0, m = 0.0;
jint iter = 0;
while ((iter < maxIter) && (m < 4.0)) {
m = r * r - i * i;
i = 2.0 * r * i + tmp;
r = m + xStart + xZoom * (jdouble) x;
++iter;
}
buffer[index++] = iter * iter;
}
}
array = (*env)->NewIntArray(env,index);
if (array == NULL) {
free(buffer);
return NULL;
}
(*env)->SetIntArrayRegion(env,array,0,index,(jint *)buffer);
free(buffer );
return array;
}
FORTRAN77 Source:
c
c fractal demo
c written by Peter Sauer
c
integer function fcalc(array,yoffset,lines,width,maxiter,xstart,
& xzoom,ystart,yzoom)
implicit none
integer array(*)
integer yoffset,lines,width,maxiter
double precision xstart,xzoom,ystart,yzoom
integer y,x
integer size
double precision tmp
double precision r,i,m
integer iter,index
size = yoffset + lines
y = yoffset
index = 1
while(y .lt. size) do
tmp = ystart + yzoom * y
x = 0
while (x .lt. width) do
r = 0.0
i = 0.0
m = 0.0
iter = 0
while((iter .lt. maxiter) .and.
& (m .lt. 4.0)) do
m = r * r - i * i
i = 2.0 * r * i + tmp
r = m + xstart + xzoom * x
iter = iter + 1
end while
array(index) = iter * iter
index = index + 1
x = x + 1
end while
y = y + 1
end while
fcalc = index
end
Assembler Source:
/*
* fractal demo
* written by Peter Sauer
* ScienceSoft 2003,2004
*/
JNIEXPORT jintArray JNICALL Java_fractal_NativeASMWorkerThread_doCalc(
JNIEnv *env, jobject obj,jint yOffset, jint lines, jint width, jint maxIter,
jdouble xStart, jdouble xZoom, jdouble yStart, jdouble yZoom) {
jint size = lines * width;
jint *buffer = (jint *)malloc(size * sizeof(jint));
jintArray array;
jint end = yOffset + lines;
int x;
int four = 4;
if(!buffer) {
return NULL;
}
_asm {
push esi // save all working registers
push edi
push eax
push ebx
push ecx
push edx
finit
mov esi,buffer // load image buffer address
mov edi,yOffset // load y-offset
fld xZoom
fld xStart // push xStart
yloop:
xor ebx,ebx // x value counter
mov x,ebx // save x value
// pre-calculate: tmp = yStart + yZoom * (double) y;
fld yStart // push yStart st
fild yOffset // push y-value st(1)
inc yOffset // increment y-value
fld yZoom // push yZoom
fmul // st = yZoom * (double) y
fadd // st = yStart + yZoom * (double) y
xloop:
xor ecx,ecx // iter = 0
fldz // i = 0
fldz // r = 0
iteration:
fld st(1) // push i
fld st
fmul // st = i * i
fld st(1) // push r
fld st
fmul // st = r * r
fsubr // m = r * r - i * i;
ficom four // m < 4?
fstsw ax
sahf
ja quit_iteration
fld st(1) // push r
fmulp st(3),st // i = i * r
fld st(2) // push i * r
faddp st(3),st // i+= i
fld st(3) // push yStart + yZoom * (double) y
faddp st(3),st // i+= yStart + yZoom * (double) y
fstp st(1)
fld st(3) // push xStart
fadd
fld st(4) // push xZoom
fild x // xZoom * x
fmul
fadd // r+= xZoomm * x
inc ecx // inc iter
cmp ecx,maxIter // iter < maxIter?
jl iteration
jmp skip
quit_iteration:
inc ecx
fstp st(0) // remove m from stack
skip:
fstp st(0) // remove i from stack
fstp st(0) //
mov eax,ecx // iter
mul ecx
mov [esi],eax // store color value
add esi,4 // increment memory index
inc x
inc ebx // increment x
cmp ebx,width // x < width
jl xloop
inc edi
cmp edi,end
fstp st(0) // remove tmp from stack
jl yloop // y < end
pop edx
pop ecx
pop ebx
pop eax
pop edi
pop esi
}
array = (*env)->NewIntArray(env,size);
if (array == NULL) {
free(buffer);
return NULL;
}
(*env)->SetIntArrayRegion(env,array,0,size,(jint *)buffer);
free(buffer);
return array;
}
Remarks
For the interpretation of the thread runtimes the following technical facts must
be taken into account:
-
As this demonstration runs on a single-processor system, the parallelization by
means of threads does not yield any advantage with regard to speed.
-
In contrast to the Java-Thread, the threads that are coded in C, FORTRAN77 and Assembler have to use JNI
(Java Native Interface) to pass on the computed graphics data to the servlet.
Given the short computation times, this interaction can lower the speed advantages of the native
programming languages compared with the JIT (Just In Time) Java-Code.
-
Mandelbrot sets that are computed by means of the manually coded Assembler-Codes can differ from the results
of the other programming languages (Java, C and FORTRAN77) in subtle graphical details. The assembler-code performs
the computations continuously with 80-bit-accuracy via the stack of the FPU (Floating Point Unit),
whereas the compiled code of the other programming languages deposits interim results of
the FPU in the store (2*32 = 64 Bit). As a point of the Mandelbrot set is defined by a
recursion, the difference in computational accuracy (64/80 Bit) can lead to a different point colour.
Mathematical background
This well-known fractal is based on the simple recursive function z = z2 + c
with the initial value z0 = 0 and c being the constant. z and
c correspond to complex numbers that can also be represented as points on the plane.
For the computation this recursion is performed for a finite set
of points of this plane. The recursion of a point can behave as follows:
-
The values of a point do not leave a certain interval - the values remain finite. In this case
the point belongs to the so-called Mandelbrot-set* and it will be
assigned the colour black.
-
If the values of the point approach infinity, the point will not be an element of the
Mandelbrot set, and its colour will compare to the number of iterations, after which its values approach infinity.
*
The set is named after the French mathematician Benoît Mandelbrot,
who was the first to generate this kind of pictures with the aid of a computer.